Resonance, the amplification of vibrations at a system's natural frequency, can lead to catastrophic failures. This guide provides a practical method—the "factor of 2 rule"—to mitigate this risk, along with advanced techniques and considerations for complex systems. We will cover how to apply this rule effectively, incorporating damping variations for more accurate predictions. For a deeper understanding of natural frequency calculations, see this helpful resource on natural frequency formulas.
Understanding Resonance and its Consequences
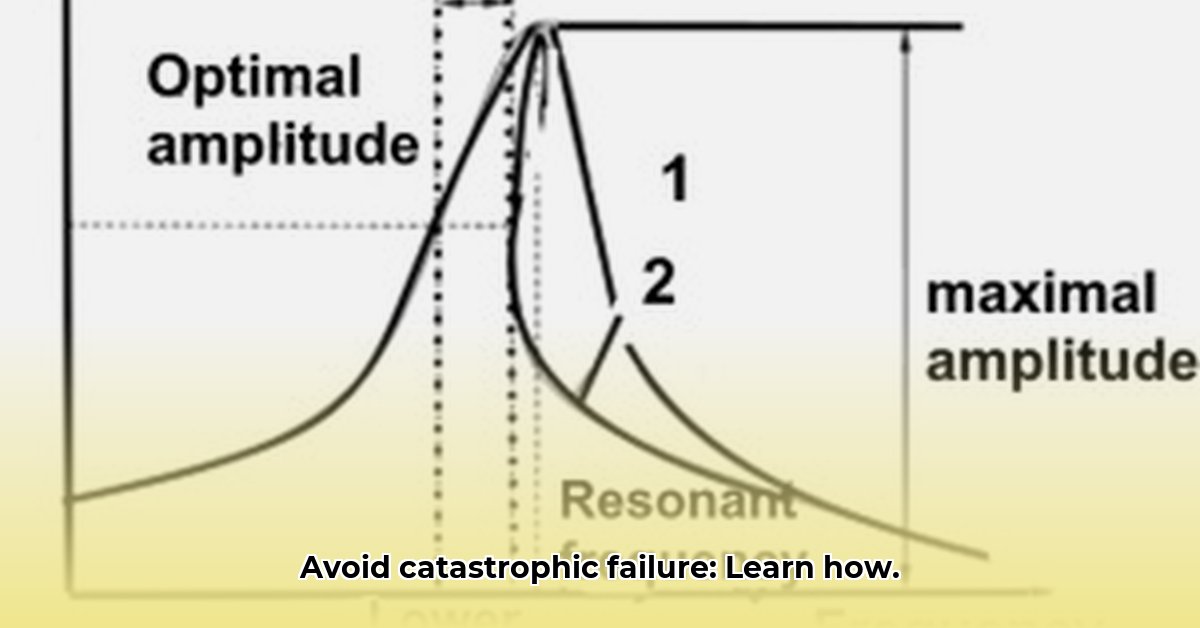
Resonance occurs when a system's natural frequency aligns with an external forcing frequency, causing dramatically increased vibrations. This can lead to fatigue failure, component malfunction, or even complete structural collapse. For example, a bridge swaying in the wind at its natural frequency might experience catastrophic failure. Preventing resonance is crucial for ensuring the safety and longevity of engineered systems.
The Factor of 2 Rule: A Practical Approach
A simple yet effective starting point for resonance avoidance is the "factor of 2 rule." This guideline suggests maintaining a minimum separation between the system's operating frequency and its lowest natural frequency. Specifically: keep the operating frequency at least twice the lowest natural frequency. By creating this frequency gap, you significantly reduce the risk of resonance.
"The factor of 2 rule is a valuable initial step, but it's crucial to understand its limitations and why more sophisticated analysis might be needed for complex systems," says Dr. Anya Sharma, Professor of Mechanical Engineering at MIT.
Applying the Factor of 2 Rule: A Step-by-Step Guide
Applying the factor of 2 rule effectively involves these key steps:
Determine Natural Frequencies: Use Finite Element Analysis (FEA) (a computer simulation method for predicting how a product reacts to real-world forces, vibration, heat, fluid flow, and other physical effects) or experimental modal testing (a method of determining a structure’s natural frequencies and mode shapes) to identify the system's natural frequencies (frequencies at which a system naturally vibrates). These frequencies depend on the system's mass, stiffness, and geometry.
Identify Operating Frequencies: Determine the frequencies at which your system will operate. This involves analyzing potential vibration sources like motors, pumps, or external forces (wind, traffic).
Frequency Comparison: Compare the operating and natural frequencies. If the operating frequency is at least twice the lowest natural frequency, you have a sufficient safety margin.
Damping Consideration: If the factor of 2 isn't met, adding damping materials (materials that absorb vibrational energy) can reduce vibration amplitudes. Examples include certain rubbers or specialized polymers.
Real-World Testing: Validate your design through real-world testing to account for real-world complexities not fully captured in simulations.
Limitations of the Factor of 2 Rule
The factor of 2 rule serves as a helpful initial guideline, but its simplicity limits its applicability in complex scenarios. For instance:
- Damping: The rule doesn't explicitly account for damping, which significantly affects resonance behavior. Higher damping reduces the system's sensitivity to frequencies near its natural frequency.
- Non-linearity: Real-world systems often exhibit non-linear behavior, deviating from the linear assumptions underpinning the factor of 2 rule.
- Multiple Modes: Complex systems have multiple natural frequencies, requiring the rule's application to each relevant mode.
- Uncertainty: Material properties, damping characteristics, and boundary conditions introduce uncertainties that necessitate conservative design.
Advanced Resonance Prevention Techniques
For complex systems, more sophisticated methods are necessary: advanced FEA (incorporating non-linear effects and damping), modal testing, vibration isolation, and active vibration control. Active vibration control uses sensors and actuators to counteract vibrations actively.
Risk Assessment Matrix
The risk of resonance varies across systems. Consider this matrix:
| System | Resonance Likelihood | Failure Severity | Recommended Mitigation Strategies |
|---|---|---|---|
| Simple Mechanical System | Low | Minor | Factor of 2 rule, component selection |
| Automotive Engine Mounts | Medium | Moderate | Factor of 2 rule, damping materials, FEA modeling |
| Aircraft Wings | High | Critical | Advanced FEA, rigorous testing, vibration isolation, active control |
| Turbine Blades | High | Critical | Advanced design optimization, specialized materials, modal testing |
| Precision Manufacturing Equipment | Medium | Moderate | Vibration isolation, robust mounting, meticulous design |
Refining the Factor of 2 Rule: Incorporating Damping
The factor of 2 rule needs refinement to account for damping. A higher damping ratio means less sensitivity to frequencies near the natural frequency. While a precise formula is elusive, a conservative approach involves increasing the safety margin (e.g., using a "factor of 3" or higher), especially when damping or natural frequency uncertainty is significant. Always validate your design with experimental data and detailed FEA that explicitly models damping.
Conclusion
Preventing resonance requires a holistic approach combining careful design, thorough analysis, and real-world testing. The factor of 2 rule is a helpful starting point, but for complex systems, advanced techniques and thorough risk assessments are crucial. Prioritizing resonance prevention avoids costly repairs, downtime, and potential safety hazards.